Jun's Blog
기본 용어 간단 정리 및 실습 -(1) 본문
1. 결측치
결측치(Missing Value)란 데이터 분석에서 값이 누락된 데이터를 의미합니다.
즉, 특정 변수나 열에 대해 값이 존재하지 않거나 측정되지 않은 경우를 말합니다. 결측치는 데이터의 품질에 영향을 미칠 수 있으며, 분석 및 모델링 과정에서 적절한 처리가 필요합니다.
import pandas as pd
import numpy as np
data ={
'a': [1, 2, np.nan, np.nan, 5], # 결측치 2개
'b': [np.nan, 2, np.nan, 4, np.nan] # 결측치 3개
}
df = pd.DataFrame(data)
print(df)
print(df.info())

missing_value_count = df.isna().sum()
print(missing_value_count)
df_filled = df.apply(lambda col : col.fillna(col.mean())) # 결측치 데이터 평균값으로 대체
print(df_filled)
print(df_filled.info)
<결측치 데이터 처리 대안>
결측치 데이터 삭제
: 결측치가 있는 행이나 열을 삭제하는 방법입니다.
결측치 데이터 대체
: 결측치를 평균, 중앙값, 최빈값, 예측된 값 등으로 대체할 수 있습니다.

1. 이상치
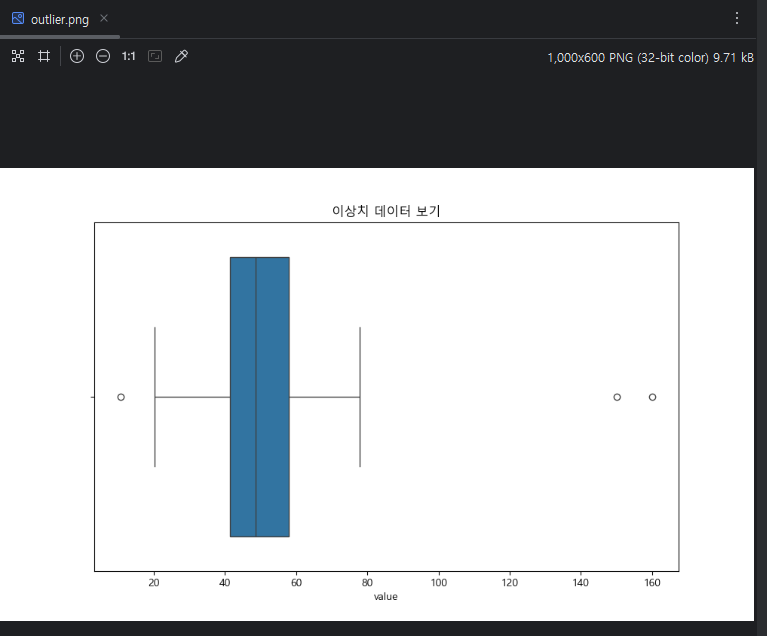
이상치(Outlier)란, 주어진 데이터 집합에서 다른 데이터들과 비교했을 때 매우 다르거나 눈에 띄게 튀는 값들을 말합니다.
상자 수염 그래프(Box Plot)는 데이터의 분포, 중심 경향성, 변동성, 이상치 등을 시각적으로 표현하는 그래프입니다. 주로 데이터의 중앙값, 사분위수, 최소값, 최대값을 나타내며, 데이터가 어떻게 퍼져 있는지를 한눈에 파악할 수 있게 도와줍니다. 이 그래프는 특히 이상치(outliers)를 쉽게 식별할 수 있는 장점이 있습니다.
# 평균 표준 편차 15를 갖는 100개의 랜덤 데이터 생성
data = np.random.normal(loc=50, scale=15, size=100)
print(data)

np.random.seed(42) # 랜덤 데이터에 대한 seed를 지정함. 매번 동일한 랜덤 결과가 나옴.

# sorted는 정렬을 수행해주는 파이썬 내장 함수
mylist = [float(item) for item in sorted(data)]
print(mylist)
[10.703823438653835, 20.186466280986608, 20.604948141803366, 21.300796330133032, 23.55439766955899, 24.126232512304508, 27.822170144488588, 28.04727577801822, 28.628777206798148, 28.815444479970626, 30.077209266523543, 31.687345250434667, 32.05690063878994, 32.73509633866546, 33.40497538990958, 34.13433606566149, 34.80753319498364, 36.37963886718184, 37.41173715166042, 37.87259595660218, 39.20233687407937, 39.469203591839715, 39.84616999541062, 40.323203680923136, 40.97440081655905, 40.99041965121793, 41.56568706138541, 41.834259132122256, 42.05359694349442, 42.22594672589529, 42.47364434623195, 42.81238643232065, 42.95788421097572, 43.01405369644615, 43.04873460781307, 43.09041843560319, 44.118377703017636, 44.22376579375525, 45.085067801033475, 45.36181436223178, 45.48344456616067, 45.51488974301199, 45.62459375310085, 46.481192999372794, 46.48769937914996, 46.487945645762295, 46.61335549270196, 46.70492168243732, 47.215115350042744, 47.92603548243223, 48.265275764176394, 48.91984817629499, 49.46260941335073, 49.79754162893099, 50.07670184963691, 51.012923070318855, 51.30570602357257, 51.37641164803254, 51.456163240220604, 51.663838845647994, 52.57052421784956, 52.952918538036855, 53.132953925071334, 53.629434073490515, 53.91582908269834, 54.44180415596864, 54.71370998892911, 54.86125954092192, 54.93126664489527, 54.96895147105346, 55.15427434352692, 55.3566885726762, 55.42093408262621, 55.424540375714514, 55.63547027518508, 57.450712295168486, 57.699011496700344, 58.13840065378947, 59.175144332613016, 59.715328071510385, 61.07699869993115, 61.51152093729363, 62.18788733591297, 62.32853756562836, 62.338173681547836, 63.731031765531114, 63.96920178674298, 64.52967485799334, 64.63317690683539, 65.05299346838036, 65.46499283743927, 65.85683339328374, 70.34360042856234, 71.98473153382331, 72.16841067112274, 72.84544784612038, 73.07054849698955, 73.4696548372101, 73.68819223261087, 77.78417276763406]
df = pd.DataFrame({'value':data})
print(df)

plt.rc('font', family='Malgun Gothic')
plt.figure(figsize=(10, 6))
sns.boxplot(x=df['value'])
plt.title('이상치 데이터 보기')
plt.savefig('outlier.png')
3. 공분산
공분산(covariance)이란 확률 변수 X의 증감에 따른 Y의 증감의 경향에 대한 척도를 말합니다.
즉, 2개의 확률 변수의 상관 정도를 나타내는 값입니다.
공분산 구하는 공식 :
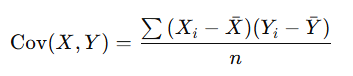
**피어슨 상관계수(Pearson Correlation Coefficient)**는 두 변수 간의 선형적인 관계를 측정하는 통계적 지표입니다. 이 값은 두 변수 간의 상관 정도와 방향을 나타내며, -1에서 1 사이의 값을 가집니다.
공분사의 상관 계수 구하는 공식:

x = [3, 5, 8, 11, 13, 8]
y = [1, 2, 3, 4, 5, 3]
count = len(x) # 데이터 개수
# 평균 구하기
# sum 함수는 총합을 구해주는 파이썬 내장 함수
bar_x = sum(x) / count
bar_y = sum(y) / count
for xi, yi in zip(x, y):
print('xi=' + str(xi), end='')
print(', yi=' + str(yi))
bunja = sum((xi - bar_x)*(yi - bar_y) for xi, yi in zip(x, y))
bunmo = count - 1
cov_xy = bunja / bunmo
print(f'공분산 : {cov_xy}')

df = pd.DataFrame({'x':x, 'y':y})
cavariance = df['x'].cov(df['y'])
print(f'파이썬 함수를 이용한 공분산 결과 : {cavariance}')

std_x = (sum((xi - bar_x) ** 2 for xi in x) / (count - 1)) ** 0.5
std_y = (sum((yi - bar_y) ** 2 for yi in y) / (count - 1)) ** 0.5
# 상관 계수 = 공분산 / (x표준편차 * y표준편차)
correlation_coefficient = cov_xy / (std_x * std_y)
print(f'상관계수 : {correlation_coefficient}')
correlation = df['x'].corr(df['y'])
print(f'파이썬 함수를 이용한 상관계수 결과 : {correlation}')
임의 데이터를 활용한 heatmap 만들어보기
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
dataIn = './../dataIn/'
df = pd.read_csv(dataIn + 'auto-mpg.csv', header=None)
df.columns = ['mpg', 'cylinders', 'displacement', 'horsepower', 'weight', 'acceleration', 'model year', 'origin', 'name']
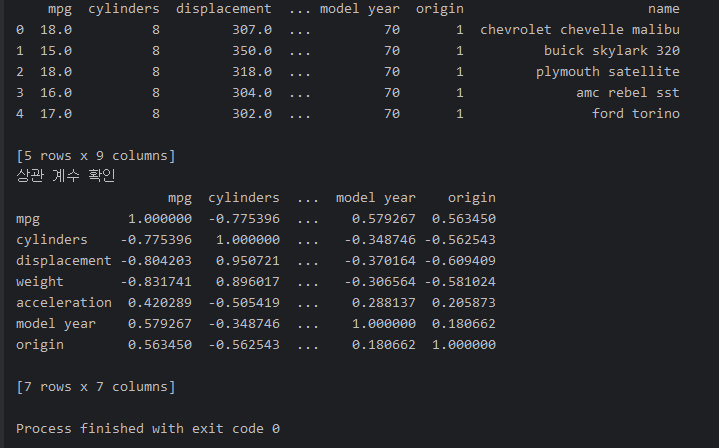
print(df.head())
print('상관 계수 확인')
corr = df.corr(numeric_only=True)
print(corr)
dataOut = './../dataOut/'
plt.figure((figsize(10, 8)))
plt.rc('font', family='Malgun Gothic')
sns.heatmap(corr, cmap='coolwarm', annot=True, fmt='.2f', cbar=True)
plt.title('변수들간 상관 계수', size=15)
plt.savefig(dataOut + 'correlation.png')

'Python > 머신 러닝' 카테고리의 다른 글
| 클래스 분류와 KNN의 활용 예시 (0) | 2025.03.21 |
|---|---|
| 클래스 분류의 정의와 SVM의 활용 예시 - (2) (0) | 2025.03.20 |
| 클래스 분류의 정의와 SVM의 활용 예시 - (1) (0) | 2025.03.20 |
| 다중 회귀 분석 및 활용 예시 (0) | 2025.03.20 |
| 기본 용어 간단 정리 및 실습 -(2) (0) | 2025.03.19 |




